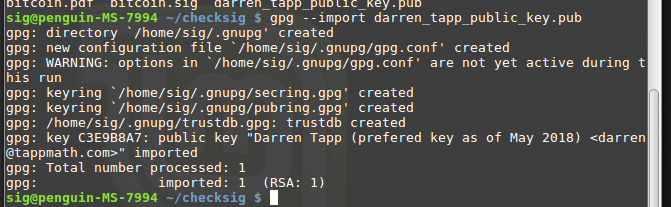
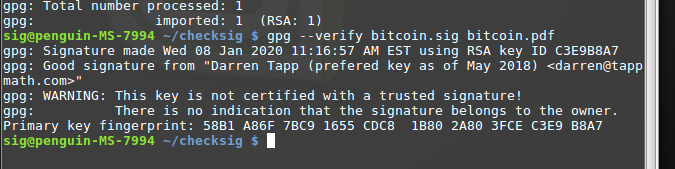
A Short Introduction to LaTeX
\( \LaTeX \) is a markup language that is used for most mathematical writing. There is really no better way to communicate mathematics. The result is really polished. It doesn't matter if you're talking about Maxwell's equations: \[ \nabla \cdot E = \frac{\rho}{\varepsilon_0} \\ \nabla \cdot B = 0 \\ \nabla \times E = - \frac{\partial B}{\partial t} \\ \nabla \times B = \mu_0 \left( J + \varepsilon_0 \frac{\partial E}{\partial t} \right), \] Schrödinger's equation \[ i \hbar \frac{\partial}{\partial t} \Psi = \left[ \frac{-\hbar^2}{2m}\nabla^2 + V \right] \Psi, \] or \(L:V\to W\) a linear map from \(V\) to \(W\). I can not think of a better way of rendering mathematics than with \(\LaTeX\). Even more valuable than looking pretty, \(\LaTeX\) is typed without using the mouse. Being able to simply type mathematics really is a joy.
Now, \(\LaTeX\) is not something that you just sit down and learn. I find it best to have in mind what you want to write before you write it. Then look up what you need to write your document. The hardest part is starting. It can really help to have an example. It's even better to make changes and see what the result is. Below I believe is a good example of a document that helps explain what \(\LaTeX\) can do and how to do it. I also have linked to the resulting document below the source.
\documentclass{article} \usepackage{amssymb} \usepackage{amsmath} \title{Example \LaTeX\ Document} \author{Darren Tapp} \date{\today} \newcommand{\RR}{{\mathbb R}} \begin{document} \maketitle \LaTeX\ is a markup language that is intended to produce beautiful mathematics. We can display an equation; \[ x+3 = 5. \] or mathematics could be in line as $x=2$. \textbackslash\ usually preceeds a command. \$ is also a special symbol that denotes math mode. One dollar sign for $\sum_{i=1}^n i$ if you want the text inline. Two dollar signs if you want to display $$ \frac{\partial \psi }{\partial t} . $$ However I prefer \textbackslash [ and \textbackslash ] to display equations. Do you want to define a linear map $L:{\mathbb R}^2\to {\mathbb R}^3$? We could could let $L$ be an embedding of ${\mathbb R}^2$ into ${\mathbb R}^3$. \[ (x,y) \mapsto (x,y,0) \] Note I get tired of typing \verb|{\mathbb R}| so I defined a macro above. I now can type about $\RR$ all day long. For some reason I would like to give an example of a matrix. \[ \begin{bmatrix} 1& 1& 0 \\ 0& 1 & 2 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = \begin{bmatrix} 3 \\ 8 \\ 3 \end{bmatrix} . \] This document uses two packages with the \verb|\usepackage| declaration above. \verb|amssymb| is used for the blackboard bold $\RR$. \verb|amsmath| is used to make the matrices easier to type. \end{document}
Here's the resulting output. If you want more information I find The Not So Short Introduction to LaTeX2e to be a close to exhaustive resource.
 Darren Tapp
Darren Tapp